Introduction to R 2

General information

Main objective

In this lecture we will continue to learn R. We will learn how to use functions and how to visualize data.

Learning objectives

• Students can use functions in R and are able to write their own

• Students can visualise data using base R plotting functions

• Students can control the flow of their programs

• Students can load packages to extend the functionality of R

Resources

This section requires the use of the R Workbench.

Functions

R does more than just simple calculations or allowing you to import and look at data. Its power comes from functions. There is a wide selection of different functions in R, some of them are built into R and some of them can be made accessible by downloading packages.

Basic functions

A function requires input arguments, some necessary, such as the data you want to run the function on, and some optional, such as the choice of method or additional parameters. As most optional arguments already have a pre-set default value it can be tricky to grasp how many arguments the function has. We will now look at a very simple first function mean in R.

First, if we want to understand a function, we read its help file.

# Get help
?mean

This prints out the documentation of that function. The first paragraph provides a description of what the function does. The second paragraph shows how to use the function in your script or the console. It also explains if there are any default values set for any of the arguments. The third paragraph takes you through all the different arguments and explains each of them. In our example, the only necessary argument x is an object that we want to apply this function to. The paragraph called Value explains what the output of the function will be. At the very bottom of the documentation you can also find some examples of how to use the function. If we don’t even know if a function exists, we can use the double question mark to search for key words

# Search keywords
??substring

Now let’s start using the mean function with a vector that contains all numbers from 1 to 10. Arguments for a function can be declared both by their position or their name. A function expects to see the arguments in a specific order, so the first argument without a name is expected to be the first argument in the function. As already discussed, the mean function only needs one input argument x.

# Find the mean of a vector
v <- 1:10
# Method 1: using the predefined postions
mean(v)
# Method 2: declare input by name
mean(x = v)

Exercises

• try calculating the sum of the same vector using the sum function

• extract the length of the vector using the length function

• calculate the mean using the results from the first two exercises and compare it to the result using mean. Can you see how using functions reduces the length of your code?

• calculate the median of the vector using the median function

We will use the swiss data set to test the mean function again. First, we will have a look at what this data set contains.

# Loading swiss data set
data(swiss)

# View swiss data set
View(swiss)

# Calculating mean for fertility
# Method 1: using the predefined postions
mean(swiss$Fertility)

# Method 2: declare input by name
mean(x = swiss$Fertility)

Let’s look at another function called sd. Sd calculated the standard deviation.

# Calculating standard deviation for fertility
sd(swiss$Fertility)

You can also use a function to find the object with the largest or smallest value in a vector using the max or min function.

# Finding the maximum and minimum of fertility
max(swiss$Fertility) #= 35
min(swiss$Fertility) #= 92.5

Exercises

Explore the swiss data set. The following questions can guide you:

• How catholic is the region with the highest fertility?

• Is there a difference in infant mortality between low-education and high education areas? (hint: define high as > 10 and low as <= 10)

• Is education higher in regions with lower agriculture? (hint: use min , max and mean, define low agriculture <= 50)

Functions and class

Many R functions are written so that they behave differently depending on what class of variable they are given. For instance, the summary function gives additional information about a variable, and what it shows depends on the variable’s class.

# Class discrimination
x <- 1:10
summary(x)

data(swiss)
summary(swiss)

data(Titanic)
summary(Titanic)

So when a function does something unexpected, consider what mode or class the variables you gave it have.

Statistical functions

R also provides a large range of statistical functions. A commonly used one is the correlation function cor. Again, have a look at the documentation to learn what the input arguments for this function need to be.

# Look at documentation
?cor

The documentation tells us that we need at least one argument x. The default correlation method is set to pearson. Let’s say we want to investigate if there is a correlation between fertility and catholic.

cor(swiss$Fertility, swiss$Catholic)

The function gives you a correlation 1x1 matrix. Your inputs do not necessarily have to be vectors, you can also input an entire matrix or data frame.

# Correlation between the entire swiss data frame and fertility
cor(swiss, swiss$Fertility)

Next, we will change the correlation method (check out the documentation again to see which ones you can pick from).

# Change method
cor(swiss$Fertility, swiss$Catholic, method = "spearman")

You can also use R for significance testing. There is a huge amount of statistical tests available. We will only have a look at the t.test function at this point. Have a look at the iris data set.

# Load iris data set
data(iris)
# iris data set
View(iris)

We now want to see if there is a significant difference in petal length between the two species setosa and versicolor. The t.test function calculates a “Welch Two samples t-test”.

# Calculate t test
t.test(iris[iris$Species == "setosa",]$Petal.Length, iris[iris$Species == "versicolor",]$Petal.Length)

This will print out the summary of the t test in your consol. If you are planning on using the output for further calculation or simulations it makes sense to store the result in a variable.

# Calculate t test and save in variable t_test
t_test <- t.test(iris[iris$Species == "setosa",]$Petal.Length, iris[iris$Species == "versicolor",]$Petal.Length)

The output is now stored as a list called t_test. You can easily access the different quantities using the dollar sign or double square brackets. For example, we can extract the t-statistic from our calculation

# Get t-statistics
t_test$statistic
t_test[["statistic"]]

To get an overview of all quantities provided by the function you can use the names function.

# Overview over all quantities
names(t_test)

Exercises

Go back to your results in exercise 2. Are the results statistically significant?

Linear Regression

R also has inbuilt functions that allow you to fit your data to a defined model. For example, lm fits a linear model determined by a formula provided. Check out the documentation to find out what arguments you need.

# Get documentation
?lm
# Linear model of the form y = m*x +c
fit <- lm(Sepal.Length ~ Petal.Width, data = iris)

To get the output of the fit use the summary command.

summary(fit)

Basic Plotting

Frequently, you will want to visualise your results. For example, we would now like to plot the linear regression fit we calculated before.The most basic plotting function in R is plot. It has many adjustable parameters which makes it a great tool to construct your plot just as you like it. First, have a look at all the possible arguments for plot.

# Get documentation
?plot

Then, we plot the petal width on the x axis against the sepal length on the y axis. Plot will automatically name the axis according to the input data but you can easily change the names of the axis. We will also give our plot a title to keep things nice and tidy.

# Plotting
plot(iris$Petal.Width, iris$Sepal.Length,                   # Define data to be plotted
     xlab = "petal width", ylab = "sepal length",           # Change name of axis
     main = "petal width vs sepal length")                  # Add plot title

Next, you can change the point shape, colour and size to your taste. Here’s an overview of the different shapes:

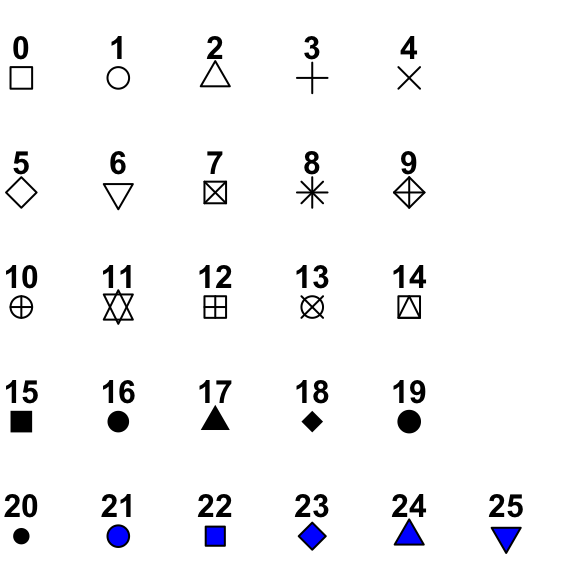
plot(iris$Petal.Width, iris$Sepal.Length,
xlab = "petal width", ylab = "sepal length",
main = "petal width vs sepal length",
pch = 16,                                                 # Change shape of data points
cex = 0.4,                                                # Change size of data points
col = "black")                                         # Change colour of data points

Now, we want to add our fit to the data. For this we will use the command abline. Abline(a,b) draws a straight line with intercept a and slope b. You can also change the colour, width and line type of abline. Here’s an overview of the different line types available:

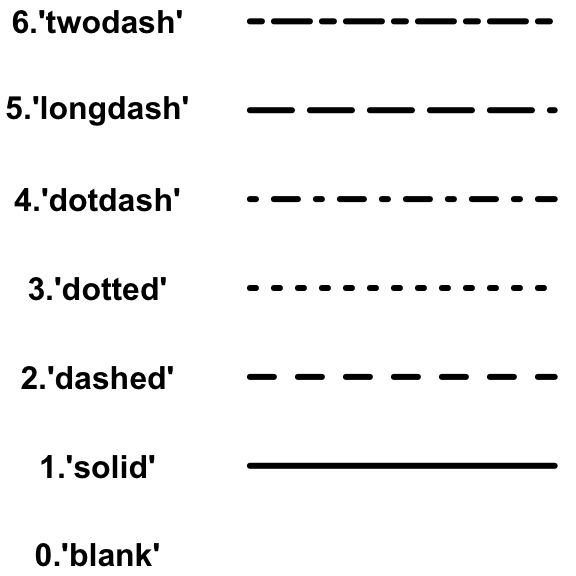
plot(iris$Petal.Width, iris$Sepal.Length,
xlab = "petal width", ylab = "sepal length",
main = "petal width vs sepal length",
pch = 16,
cex = 0.4,
col = "black")
abline(fit,                                               # Drawing a line with the coefficients of fit
       col = "red",                                    # Change colour of line
       lty = "solid",                                     # Change line type
       lwd = 1)                                           # Change line width

Now, last but not least, we would like to add a legend showing the adjusted r squared value of the fit. We can extract this information from the fit summary.

# Summary of lm fit
summary_fit <- summary(fit)
# Get adjusted R^2 value
r2 <- summary_fit$adj.r.squared
# Create a legend text
mylabel = bquote(italic(R)^2 == .(format(r2, digits = 3)))   # bquote enables us to use mathematical expressions, digits = 3 rounds the                                                                  # result to 3 decimal places.
legend('topleft',                                            # Defines position of legend
       legend = mylabel,                                     # Define text for legend
       cex = 0.7,                                            # Define size of legend
       bty = "n")                                            # "n" = no boxline for legend, "o" = boxline for legend

That’s it, your first plot in R!

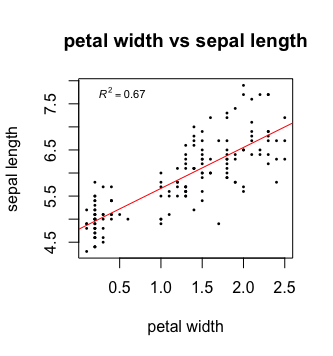
In some cases, it can be helpful to manipulate the x and y axis. For examples, you can set boundaries or log transform the axis.

# Changing axis
plot(iris$Petal.Width, iris$Sepal.Length,
    xlim = c(0,12),                                        # xlim = c(boundry_left, boundry_right)
    ylim = c(0,12))                                        # ylim = c(boundry_down, boundry_up)

# Log transformation
plot(iris$Petal.Width, iris$Sepal.Length,
    log = "x")                                             # Transforming x axis. use log = "xy" to transform both

Exercises

• Go back to the swiss data set and use the functions you have learned to find the best correlation between variables

• Use linear regression to model the relationship between the two variables and determine its significance

• Present your result with a suitable plot

Program Flow

Without controls, a program will simply run from top to bottom, performing each command in turn. This would mean writing a lot of code if you wanted to perform the same set of actions on multiple different sets of data. Here we will learn how to control which parts of a program execute with if, and how to perform repetitive actions with the for loop.

The if function

An if function performs a logical test – is something TRUE? – and then runs commands if the test is passed.

# If function
x <- 4
if(x >= 0){
    y = sqrt(x)
}

Here, we only want to calculate the square root of x if x is positive.

We can extend the use of if to include a block of code to execute if something is FALSE.

# If / Else
x <- -2
if(x >= 0){
    y = sqrt(x)
}else{
    cat("The result would be a complex number!")
}

You can go further by making if dependent on multiple logic statements, or use recursive if statements.

# Only allow integer square roots
x <- 4.2
if((x >= 0) & (x%%1==0)){
    y = sqrt(x)
}else{
    cat("The result would not be an integer!")
}

# Alternative method
if(x >= 0){
    if(x%%1==0){
        y = sqrt(x)
    }else{
        cat("The result would not be an integer!")
    }
}else{
    cat("The result would be a complex number!")
}

Exercises

• In the script window, copy the first if statement above and execute it. You should get the correct result, 2.

• Now make x a negative value and execute the script again, what happens?

• Add an else statement to your script as in the second example above and test it.

• Using either multiple logic statements or nested if statements, write a script that tests whether x is an even square number.

The for loop

Whilst it’s very simple to run basic calculations on a vector or matrix of data, more sophisticated code is required for data.frames or when you want to perform complex functions on individual pieces of data.

The for loop is a basic programming concept that runs a series of commands through each loop, with one variable changing each time, which may or may not be used in the loop’s code. For instance we could loop through the numbers 1 to 10 if we wanted to perform an action 10 times, or if we wanted to use the numbers 1 to 10 each in the same calculation.

# A basic for loop
for(i in 1:10){
    cat("Loop!")
}

# A loop involving the loop variable
for(i in 1:10){
    cat(paste("Loop",i,"!"))
}

These are simple examples and don’t capture the results of the loop. If we want to store our results, we have to declare a variable ahead of time to put them into.

# A loop that gets results
data(EuStockMarkets)
plot(EuStockMarkets[,1])
movingAverage <- vector()
for(i in 1:length(EuStockMarkets[,1])){
    movingAverage[i] <- mean(EuStockMarkets[i:(i+29),1])
}
plot(movingAverage)

Note that an error was produced because when we reach the end of the time series, the data points we ask for don’t exist – we could adjust our loop to account for this by reducing the number of times we go through the loop so that we don’t reach past the end of the data.

Also, rather than refer to the pieces of data directly, we are using i to keep track of the index of the data we want to work with. This allows us to refer to data by its index, and therefore slice a moving section of data. In other circumstances, you can of course refer to items by their names.

Exercises

• Write a for loop that prints out a countdown from 10 to 1.

• Using the EuStockMarkets data, make a plot of the FTSE data. Note that this data is not a data.frame but a time.series - you can find out more with ?ts.

• Using a for loop, calculate a moving average and make a corresponding vector of time points with the centres of each average.

• Add the moving average to the plot using the lines function.

The *apply functions

Consider that we might want to calculate an average of each of the data sets in the EuStockMarkets data over time. We can write a loop to do this:

# Calculate stock market average
stock_average <- c()
for(i in 1:nrow(EuStockMarkets)){
    stock_average[i] <- mean(EuStockMarkets[i,])
}

Although this seems brief, it can quickly become a lot of code when you want to work with multidimensional data, and although you won’t notice on this small amount of data, it is slow.

Instead, it would be easier to identify the function we are interested in using and simply apply it to our data.

# Using the apply function
stock_average <- apply(EuStockMarkets,1,mean)

The function works by giving it a matrix or data.frame (or here, a time.series also works), telling it whether you want to run the function across rows (1) or columns (2) and then the function you want to use. As a fourth argument you can give a list of additional arguments for the function you are running.

The apply function is for matrices and data.frames, but you can run lapply for a list, vapply for a vector, or sapply works for both.

Exercise

• Using the apply function, find the mean and standard deviation (sd) of the four data sets over time.

• Make a plot of the mean against the sd.

• Use linear regression to determine if there is a correlation between the mean and sd of this data and add a trend line to your plot.

Writing Functions

You can define your own function in R. This is particularly useful if you want to perform the same task with many different data sets. Your definition requires you to declare your function’s arguments and whether they have a set default value or not. Arguments cannot by default be forced to a certain mode or class, but you can check for them in the function an coerce them if necessary. Variables within your function are limited to only that function, and after it has run will simply disappear. If you want to store a result from a function, you must return it to the main program.

Defining a basic function

Functions always have the same structure:

function_name <- function(argument, argument = default value) {
      statement or operations
      return(result)
}

You need to define a name for your function that you will later use to call it with. The curly brackets define where the function starts and ends. The return command returns the result back to the main program. Let’s have a look at a first example. We would like to write a function that converts temperature Fahrenheit to Celsius.

# Defining function
f_to_c <- function(temp_F) {          # Define a function and argument temp_F, no default arguments
  temp_C <- (temp_F - 32) * 5 / 9     # Perform calculations using the argument
  return(temp_C)                      # Return the result to the main program
}

# Using the function
f_to_c(70) # = 21.1                   # Using the name of the function to call it

The next function decrypts numbers into letters. We define two arguments: the necessary argument x and the optional argument offset which is set to 0 by default.

# Defining a function
caesarDecrypt <- function(x,offset=0){
  new_x = x - offset - 1                  # Remove the offset and minus 1 for the next line
  new_x = new_x%%26 + 1                   # Find the modulo, add 1 to move from 0:25 to 1:26
  string = letters[new_x]                 # Translate numbers to letters
  return(string)                          # Return the answer
}
# Using it
x <- c(3,8,18,9,19)
caesarDecrypt(x)
x <- c(7,14,20,17,20,12,4)
caesarDecrypt(x, offset = 12)

You can create functions as complex as you like. For example, we can include an if statement or for loops. This next function only multiplies by 3 the input if it is an even number.

# Multiply all even number by a certain factor
OnlyIfEven <- function(number, factor = 3){             # Define function. multiplication factor is set to 3 by default
  temp_res <- number %% 2                               # Calculate modulo
  if (temp_res == 0){                                   # If modulo is zero then the number is even
  res <- number*factor                                  # Multiplication
  print(res)                                            # Print result. Careful, this does not return the result!
  }
  else{print("error: expected even number")             # Print error message if modulo not zero
}
}

# Using the function
OnlyIfEven(4) #=12
OnlyIfEven(5) #error: expected even number

Organising Functions

If you need to write many different functions for your data set it is recommended to keep them saved in separate files. This keeps your scripts nice and tidy. You can always call another file in your current script by using the source command.

source("path_to_your_file/filename.R")

Exercises

• Write a function to add up all numbers in a vector except for the highest

• Write a function that deciphers letters into numbers. (hint: use the which function)

Packages

We’ve so far used a lot of fundamental functions in R, the sort without which you couldn’t execute simple scripts at all. When performing data analysis however, there may well be better or more specific functions available for what you are trying to do. R is very flexible because it allows the loading of additional packages created by the user community to enhance and add functionality.

Loading a Package

To load a package, we use the library function. Once loaded, all of the functions inside the package become available to R. If a function should have the identical name to an existing function, it will mask the current version and refer instead to the version in the package, and give you a warning.

# For instance if we want to work with phylogenetic trees
# If you look at the example.tree file itself you can see the format is non-intuitive
library(ape)
tree <- read.tree("/science/teaching/example.tree")

# Packages can load other packages and mask functions
library(Hmisc)

Installing a Package

For native R packages, the install.packages function allows installation of new packages into a personal user library.

# Install a new package
install.packages("beeswarm")

# Load the package and demonstrate
library(beeswarm)
random_numbers <- rnorm(100)
beeswarm(random_numbers)
beeswarm(random_numbers,method="hex")

If the package has not been submitted to the standard R repositories, but exists for instance on github, the package devtools allows you to install it directly - you may have to install it yourself using the method above.

# Load devtools
library(devtools)

# Install a package from github
install_github(https://github.com/Gibbsdavidl/CatterPlots)

# Load the package and demonstrate
library(catterplots)
x <- rnorm(10)
y <- rnorm(10)
multicat(x,y)

Bioconductor

Bioconductor is a popular set of specific bioinformatics tools, such as DESeq2 and Biostrings, that need to be installed via the BiocManager package.

# First of all install the manager
install.packages("BiocManager")

# Use it directly without loading
BiocManager::install("Biostrings")

# Load the package and demonstrate
library(Biostrings)
cdss <- read.DNAStringSet("ecoli/EC_K12_MG1655_genomic.fna")
subseq(cdss,1,10)