Ctrl+K

Introduction to linear regression

Introduction to linear regression#

Linear Regression#

R also has inbuilt functions that allow you to fit your data to a defined model. For example, lm fits a linear model determined by a formula provided. Check out the documentation to find out what arguments you need.

#get documentation
?lm
#linear model of the form y = m*x +c
fit <- lm(Sepal.Length ~ Petal.Width, data = iris)

To get the output of the fit use the summary command.

summary(fit)

Basic Plotting#

Frequently, you will want to visualise your results. For example, we would now like to plot the linear regression fit we calculated before.The most basic plotting function in R is plot. It has many adjustable parameters which makes it a great tool to construct your plot just as you like it. First, have a look at all the possible arguments for plot.

#get documentation
?plot

Then, we plot the petal width on the x axis against the sepal length on the y axis. Plot will automatically name the axis according to the input data but you can easily change the names of the axis. We will also give our plot a title to keep things nice and tidy.

#plotting
plot(iris$Petal.Width, iris$Sepal.Length,                   #define data to be plotted
     xlab = "petal width", ylab = "sepal length",           #change name of axis
     main = "petal width vs sepal length")                  #add plot title

Next, you can change the point shape, colour and size to your taste. Here’s an overview of the different shapes:

../../../_images/r-plot-pch-symbols-points-in-r.png 
plot(iris$Petal.Width, iris$Sepal.Length,
xlab = "petal width", ylab = "sepal length",
main = "petal width vs sepal length",
pch = 16,                                                 #change shape of data points
cex = 0.4,                                                #change size of data points
colour = "black")                                         #change colour of data points

Now, we want to add our fit to the data. For this we will use the command abline. Abline(a,b) draws a straight line with intercept a and slope b. You can also change the colour, width and line type of abline. Here’s an overview of the different line types available:

../../../_images/linetypes-in-r-line-types.png 
plot(iris$Petal.Width, iris$Sepal.Length,
xlab = "petal width", ylab = "sepal length",
main = "petal width vs sepal length",
pch = 16,
cex = 0.4,
colour = "black")
abline(fit,                                               #drawing a line with the coefficients of fit
       colour = "red",                                    #change colour of line
       lty = "solid",                                     #change line type
       lwd = 1)                                           #change line width

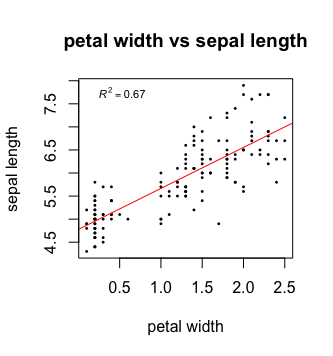
Now, last but not least, we would like to add a legend showing the adjusted r squared value of the fit. We can extract this information from the fit summary.

#summary of lm fit
summary_fit <- summary(fit)
#get adjusted R^2 value
r2 <- summary_fit$adj.r.squared
#create a legend text
mylabel = bquote(italic(R)^2 == .(format(r2, digits = 3)))   #bquote enables us to use mathematical expressions, digits = 3 rounds the                                                                  #result to 3 decimal places.
legend('topleft',                                            #defines position of legend
       legend = mylabel,                                     #define text for legend
       cex = 0.7,                                            #define size of legend
       bty = "n")                                            #"n" = no boxline for legend, "o" = boxline for legend

That’s it, your first plot in R!

../../../_images/linear_regression.png

In some cases, it can be helpful to manipulate the x and y axis. For examples, you can set boundaries or log transform the axis.

#changing axis
plot(iris$Petal.Width, iris$Sepal.Length,
    xlim = c(0,12),                                        # xlim = c(boundry_left, boundry_right)
    ylim = c(0,12))                                        # ylim = c(boundry_down, boundry_up)

#log transformation
plot(iris$Petal.Width, iris$Sepal.Length,
    log = "x")                                             #transforming x axis. use log = "xy" to transform both

Exercises#

  • Go back to the swiss data set and use the functions you have learned to find the best correlation between variables

  • Use linear regression to model the relationship between the two variables and determine its significance

  • Present your result with a suitable plot

Next: Program Flow

Contents