Refresher/Preparation R¶

General information¶

Main objective¶

This section introduces R - a programming language for statistical computing and graphics. After completion, students should have all the necessary R knowledge to participate in the course.

Learning objectives¶

Students refreshed their knowledge in R
Students can login into R-Studio
Students can work on R-Studio

Resources¶

This section requires the use of R-studio on our server. You should have therefore completed the Setup .

You can access R-Studio on our server through this link: http://cousteau-rstudio.ethz.ch/

Calculation and Variables¶

R as calculator¶

Using R at its most basic, it is a calculator. You can enter a calculation into the console and immediately evaluate the result.

# R is a calculator
1 + 2
3 * 4

Variables¶

A core concept in programming, a variable is essentially a named piece of data. That is, when you refer to the variable by its name within the program, you are actually referring to the data stored under that name.

To assign data to a variable in R, use the following syntax:

# Assignment
x <- 2
y <- 3.5

After you have assigned data to variables, you can then use the variables to perform calculations:

# R is a clever calculator
x + 2
x * y
z <- x + x + x

If you need to see the value of a variable in the command line, you can just type its name:

# What is x?
x

Note that variable names are case sensitive, and cannot start with a number.

Exercise 0.1

Experiment for yourself with the R command line to do some simple calculations

## At this stage , the main point is to write in the R console . You can try the lines under the R as a calculator section.

Assign some different numbers to the variables x and y and check if calculations with them work as you expect

#At this stage , the main ail is to create your first R script and writing the commands their . You can try the lines under variable subsection

Try to do a calculation with a variable you haven’t assigned any data to, a for instance

# calculation with previously undeclared variable
a+x
Error: object 'a' not found

Set x to 1, then check what happens when you run the calculation x <- x + 1, what value is x afterwards?

 # Set x to 1 and calculate
x <- 1
x <- x + 1
x
# 2 (autoincremants x as ++x)

Be aware that R has special values for certain calculations - try dividing by 0 for instance.

# Dividing by 0
x / 0
# Inf

Types¶

In R, and many other languages, variables also have a type, which defines the sort of data they store. R is actually a bit more complicated because it has modes and classes:

A mode is most like a type in other languages, and determines the type of data stored, such as ‘numeric’ or ‘character’.
A class is a container that describes how the data is arranged and tells functions how to work with the data.

Some modes you might encounter:

numeric - numbers, including integers and floating points numbers
character - strings
logical - TRUE or FALSE
list - a special mode for containing multiple items of any, possibly different, mode(s), whose mode becomes ‘list’

Some classes you might encounter:

vector - a one-dimensional set of items of the same mode
matrix - a multidimensional set of items of the same mode
data.frame - a two-dimensional table with columns of different modes
formula - a declaration of how variables are related to each other, for fitting models
factor - a categorical variable

The reason that it is sometimes important to know what mode and class your variable has, is that functions behave differently according to the data they are given. It’s easy to accidentally transform your variable into an unexpected format and then get an unexpected result from the functions you use in your program.

Mode detection¶

To a certain extent, R will auto-detect what mode a variable should have based on the data. There are convenient functions to check a variable’s mode when you need to.

# Auto-detection of variable mode
x <- 1
y <- "word"

mode(x)
mode(y)

# What about if we make a mistake
x <- "1"

is.numeric(x)

Vectors¶

If we want to create a variable that contains multiple pieces of data, we must make a declaration when we assign data to the variable.

# Creating a vector
x <- c(1, 2, 3)
x

# Lazy sequences
x <- 1:3
x

# Creating a vector with variables
x <- 1
y <- 2
z <- c(x, y, 3)
z

Exercise 0.2

Create a vector containing the numbers 1 to 10

# create a vector
x <- 1:10

What happens if you add 1 to this variable?

# Do some arithmetic
x + 1
# It adds 1 to each value in the vector

What happens if you multiple the variable by 2?

x*2
# It multiplies every value by 2

What happens if you add the variable to itself?

x + x
# This time it adds the first value to the first value, the second to the second, etc.

Now create two vectors of the same length containing different numbers, say 1 to 3 and 4 to 6.

# Create two different vectors
a <- 1:3
b <- 4:6

What happens when you add or multiply these together?

# Do some arithmetic
a + b
# It adds them element-wise, i.e.: first to first, etc.
a * b
# It multiplies element-wise

What happens if you add or multiply two vectors of different lengths?

# Different length vectors
a + x
# We get a warning, but it produces a result: repeating the shorter vector to have enough elements to add to the larger vector
# But let's try another
x <- 1:6
a + x
# No warning this time because the length of a (3) is a multiple of the length of x (6)
# R assumes you meant to do this, and repeats a twice to add to x

Lists and Data Frames¶

Lists¶

Vectors and matrices have the limitation that they must contain data all in the same mode, i.e.: all numbers or all characters. Lists circumvent this limitation, acting as containers for absolutely any type of data.

# Declare an empty list
l <- list()

# Declare a list with items
l <- list("a", 1, "b", 2:4)
l

# Declare a list with named items
l <- list(names=c("Anna", "Ben", "Chris"), scores=c(23, 31, 34))
l

Data Frames¶

In that last example, it would be ideal if we could link the names with the scores, and maybe further data. We can store tabular data in R in a data frame, which is really a special kind of list.

# Declare a data.frame
df <- data.frame(names=c("Anna", "Ben", "Chris"), scores=c(23, 31, 34))
df

Looking at the df, you can see that the data is neatly arranged in named columns. You can also change the format of a variable between list and data frame quite easily.

# Change between list and data.frame
l <- list(names=c("Anna", "Ben", "Chris"), scores=c(23, 31, 34))
df_from_l <- as.data.frame(l)

df <- data.frame(names=c("Anna", "Ben", "Chris"), scores=c(23, 31, 34))
l_from_df <- as.list(df)

If you then look at l_from_df, the way the list is shown includes the line ‘Levels: Anna Ben Chris’. Levels are the possible choices for a categorical factor, which is a variable mode in R for storing that sort of data. Data frames will almost always convert text into a factor, which will cause that data to behave differently than a character variable. This can be avoided:

# No factors please
df <- data.frame(names=c("Anna", "Ben", "Chris"), scores=c(23, 31, 34), stringsAsFactors=F)
as.list(df)

Exercise 0.3

Create a simple list containing some numbers - not vectors of numbers

# A list of only numbers
numbers <- list(1, 3, 6, 10)

What happens if you try to do arithmetic with the list?

numbers + 1
# We get an error - lists cannot be used like vectors!

Now create a data frame with three columns, a name and two numeric values per name, such as coordinates.

# A data frame of mixed types
coords <- data.frame(Place=c("London", "Paris", "Zurich"), Latitude=c(51.5074, 48.8566, 47.3769), Longitude=c(-0.1278, 2.3522, 8.5417))

What happens if you try to do arithmetic with the data frame?

coords + 1
# We get a result, and a warning - the data frame cannot do arithmetic with factors, but can with the numbers.

Importing Data¶

R has a host of functions for importing data of different types which I am not going to explain further. But in general, I recommend to save data tables files (for example from Excel) in a tab-delimited text manner. This makes the import into R simpler.

Firstly we need a data table to import: /nfs/teaching/551-1299-00L/R_refresher/ecoli_genes.txt. We can then use the read.table function.

# Import a data table
genes <- read.table("/nfs/teaching/551-1299-00L/R_refresher/ecoli_genes.txt")

We can now see what the table looks like using the Environment tab in the top-right - but something went wrong and the column headings are in the first row. We can fix this pretty easily.

# Import the table again
genes <- read.table("/nfs/teaching/551-1299-00L/R_refresher/ecoli_genes.txt",header=TRUE)

There are a few other useful arguments to help import tables of various formats:

sep - determines the field separator (between columns), i.e.: sep=”,”
quote - determines the quote mark (items in quote marks are considered to be the same field), i.e.: quote=”"”
row.names - determines which column contains the row names, if there are any
comment.char - determines which character, if at the start of a line, indicates the line should be ignored, i.e.: comment.char=”#”
stringsAsFactors - determines whether the table should turn text into factors, which you may want to turn off, i.e.: stringsAsFactors=F

Note

If you want to upload something from your local machine, you can use the Upload button in the Files section (window at the bottom right).

Exporting Data¶

Conversely, R has functions for exporting data into different formats. You will most likely want to create a file to open in R later, or a .csv file to open in Excel.

# Write a data.frame to an R-friendly format
write.table(df,"Rfriendly_df.txt")

# Write a data.frame to a .csv file
write.csv(df,"df.csv")

Many of the arguments for the read functions also apply to the write functions, so you can decide whether you want to see row or column headings, how the text fields are separated, etc.

Note

If you want to download the file to your local machine, right-click on the file you want to download and choose the Save as option. Select a folder on your local machine.

Names and Indexing¶

Names¶

In R, it is not just variables that have names. We have seen that data frames can have column names, and it’s also possible to give them row names. In fact, any element in a vector or list can be given a name, and these names are accesible through a simple function.

# Naming a vector
x <- 1:5
names(x) # NULL

names(x) <- c("A","B","C","D","E")
names(x) # "A" "B" "C" "D" "E"
x

This is slightly different in a matrix or data.frame, where you can name the rows and columns.

# Naming rows and columns
df <- data.frame(1:3,4:6,7:9)
df
#     X1.3 X4.6 X7.9
# 1    1    4    7
# 2    2    5    8
# 3    3    6    9

rownames(df) # "1" "2" "3"
colnames(df) # "X1.3" "X4.6" "X7.9"

rownames(df) <- c("A","B","C")
colnames(df) <- c("X","Y","Z")
df
#   X Y Z
# A 1 4 7
# B 2 5 8
# C 3 6 9

Indexing¶

Sometimes you want to refer to only part of a vector, matrix or data.frame – perhaps a single column or even single item. This is called slicing and requires an understanding of how R indexes the elements in objects.

For a vector, you can either reference an item by its position or name.

# Slicing a vector
x <- c("Chris","Field","Bioinformatician")
names(x) <- c("Name","Surname","Job")

x[1] #Name  "Chris"
x["Name"] #Name  "Chris"

For a matrix or data.frame, the same methods work for indexing the row or column of the object, or both. The convention is that first you give the row, then the column, separated by a comma, and if one is left blank it implies you want ‘all’ rows or columns. For this example we are going to load up a pre-made set of data that comes with R.

# Slicing a data.frame
data(swiss)

swiss[1,] # outputs all the elements in the first row of the swiss data.frame
swiss[,1] # outputs all the elements in the first column of the swiss data.frame
swiss[1,1] # outputs the element in the first row and first column of the swiss data.frame
swiss["Gruyere",] # outputs all the elements withtin the row named "Gruyere" of the swiss data.frame
swiss[,"Fertility"] # outputs all the elements withtin the column named "Fertility" of the swiss data.frame

Finally there are two additional ways to access items in a list, or columns (only) of a data frame.

# Accessing a list item
l <- list(names=c("Anna", "Ben", "Chris"), scores=c(23, 31, 34))
l$names #"Anna"  "Ben"   "Chris"
l[[1]] #"Anna"  "Ben"   "Chris"
l[["names"]] #"Anna"  "Ben"   "Chris"

# The difference between single and double brackets for a list
l[1] # Produces a list of one item
# $names
# [1] "Anna"  "Ben"   "Chris"

l[1:2] # Produces a list of two items
# $names
# [1] "Anna"  "Ben"   "Chris"
# $scores
# [1] 23 31 34

l[[1]] # Produces a vector
# "Anna"  "Ben"   "Chris"

l[[1:2]] # Produces a single item, the second entry in the first item in the list
# "Ben"

# Accessing a column of a data frame
swiss$Fertility
swiss[[1]]
swiss[["Fertility"]]

You can also slice multiple items by giving a vector of numbers or names. Remember that R automatically translates the code n:m into a range of integers from n to m.

# Slicing a range
x[1:2]
swiss[1:3,]
swiss[4:5,1:3]
swiss[c("Aigle","Vevey"),c("Fertility","Catholic")]

Exercise 0.4

Load the pre-made data set swiss

# Load the data
data(swiss)

Look at the row and column names, then try to rename the columns

# Look at the row and col names, try to rename
rownames(swiss)
colnames(swiss)
colnames(swiss) <- c("A","B","C","D","E","F")

What happens if you give fewer names than there are columns?

# What happens if I don't give enough names
colnames(swiss) <- c("A","B")
# The other columns are named NA, which is a problem

Create a vector containing the numbers 1 to 10 and then create a vector containing the first ten square numbers

# Create the vectors
n <- 1:10
sq <- n*n

Slice the vector to check the value of the 7th square number

# Slice the 7th square
sq[7]

Returning to the swiss data set, extract the data for just Sion

# Reload (because we renamed things) and extract data for Sion
data(swiss)
swiss["Sion",]

Now extract only the Catholic data for the first ten places, and than just for Sion

# Extract just Catholic data
swiss$Catholic
# or
swiss[,"Catholic"]
# or even, but this is less reliable if things move around
swiss[,5]

# Extract more specific data
swiss[1:10,"Catholic"]
swiss["Sion","Catholic"]

Finally use vectors to find the data on Examination and Education for Neuchatel and Sierre

# Extract very specific data
swiss[c("Neuchatel","Sierre"),c("Examination","Education")]
# Note that in the original table, Neuchatel appears after Sierre, but here they are reported in the order I gave

Logical Slicing¶

We have seen that we can give R a vector of numbers or names and it will slice out the corresponding data from a vector or data frame. We can actually go further than that and use a vector of logical values, TRUE or FALSE to determine which elements we want to slice out. Furthermore, we can write the vector as a variable ahead of time if we like.

# Slice using premade vectors
places <- c("Neuchatel","Sierre")
cols_of_interest <- c("Examination","Education")

data(swiss)
swiss[places,cols_of_interest]

# Slice using a logical
cols_of_interest <- c(FALSE, FALSE, TRUE, TRUE, FALSE, FALSE)
swiss[places,cols_of_interest]

Now the really clever bit is that we can generate a vector of logical values using the data itself, with any of the comparison functions such as >, <, ==.

# Logical slicing
isCatholic <- swiss$Catholic > 50
swiss[isCatholic,]

# Logical slicing without saving the vector ahead of time
swiss[swiss$Fertility < 50,]

Exercise 0.5

Reload the swiss data set, in case you have edited it

# Reload the data
data(swiss)

Create a vector with the column names in alphabetical order and use it to ‘slice’ the table (we are really just rearranging!)

# Create a sorted vector of column names
names_sorted <- c("Agriculture", "Catholic", "Education", "Examination", "Fertility", "Infant.Mortality")
swiss_sorted <- swiss[,names_sorted]

Slice the table to see just the places with an Agriculture score less than 50

# Find places with low agriculture
low_ag <- swiss$Agriculture < 50
swiss[low_ag,]
# or directly
swiss[swiss$Agriculture < 50,]

Now, making sure to save the results into new variables, split the table into two based on whether a place has more or less than 50 in Catholic

# Split the table by catholic score
low_cath <- swiss[swiss$Catholic < 50,]
hi_cath <- swiss[swiss$Catholic >= 50,]

In each table, look at the Catholic column data only, what do you notice about it?

# Look at the values
low_cath$Catholic
hi_cath$Catholic
# With only a couple of exceptions, the values are either very low or very high - the distribution of scores is bimodal!

Functions¶

R does more than just simple calculations or allowing you to import and look at data. Its power comes from functions. There is a wide selection of different functions in R, some of them are built into R and some of them can be made accessible by downloading packages.

Basic functions in R¶

A function requires input arguments, some necessary, such as the data you want to run the function on, and some optional, such as the choice of method or additional parameters. As most optional arguments already have a pre-set default value it can be tricky to grasp how many arguments the function has. We will now look at a very simple first function mean in R.

First, if we want to understand a function, we read its help file.

# Get help
?mean

This prints out the documentation of that function. The first paragraph provides a description of what the function does. The second paragraph shows how to use the function in your script or the console. It also explains if there are any default values set for any of the arguments. The third paragraph takes you through all the different arguments and explains each of them. In our example, the only necessary argument x is an object that we want to apply this function to. The paragraph called Value explains what the output of the function will be. At the very bottom of the documentation you can also find some examples of how to use the function. If we don’t even know if a function exists, we can use the double question mark to search for key words

# #search keywords
??substring

This will open a page called Search Results, in the Help section of the bottom right panel suggesting functions that are most likely to answer your request you can see from which library each function comes from and a short description of what it does.

Now let’s start using the mean function with a vector that contains all numbers from 1 to 10. Arguments for a function can be declared both by their position or their name. A function expects to see the arguments in a specific order, so the first argument without a name is expected to be the first argument in the function. As already discussed, the mean function only needs one input argument x.

# Find the mean of a vector
c <- 1:10
#method 1: using the predefined postions
mean(x)
#method 2: declare input by name
mean(x = c)^

Exercise 0.6

Try calculating the sum of the same vector using the sum function

#defining vector c
c <- 1:10
#calculate sum
sum <- sum(c)

Extract the length of the vector using the length function

len <- length(c)

Calculate the mean using the results from the first two exercises and compare it to the result using mean. Can you see how using functions reduces the length of your code?

mean_calc <- sum/len
show(mean_calc)
#we can see that the result of mean_calc and mean are the same.  However, we used up 3 lines to code the median. The function median       only uses one line and is much more efficient.

Calculate the median of the vector using the median function

#calculate median of c
med <- median(c)
show(med)

We will use the swiss data set to test the mean function again. First, we will have a look at what this data set contains.

#loading swiss data set
data(swiss)
#view swiss data set
View(swiss)
#calculating mean for fertility
#method 1: using the predefined postions
mean(swiss$Fertility)
#method 2: declare input by name
mean( x = swiss$Fertility)

Let’s look at another function called sd. Sd calculates the standard deviation.

#calculating standard deviation for fertility
sd(swiss$Fertility)

You can also use a function to find the object with the largest or smallest value in a vector using the max or min function.

#finding object with largest/smallest in vector x
c <- 2:30
max(c) #= 30
min(c) #= 2

Exercise 0.7

Explore the swiss data set. The following questions can guide you:

How catholic is the region with the highest fertility?

#how catholic is the region with the highest fertility
#get all columns for max fertility
swiss[swiss$Fertility == max(swiss$Fertility),]
#only get Catholic column
swiss[swiss$Fertility == max(swiss$Fertility), "Catholic"] #93.4

Is there a difference in infant mortality between low-education and high education areas? (hint: define high as > 10 and low as <= 10)

#difference in mean between high and low education areas
#slicing data frame
low_education <- swiss[swiss$Education <= 10,]
high_education <- swiss[swiss$Education > 10,]
#calculating means
mean(low_education$Infant.Mortality) #20.2
mean(high_education$Infant.Mortality) #19.48824

Is education higher in regions with lower agriculture? (hint: use min , max and mean)

#how does education affect agriculture?
#slicing data frame
low_agriculture <- swiss[swiss$Agriculture <= 50,]
high_agriculture <- swiss[swiss$Agriculture > 50,]
#calculating means
mean(low_agriculture$Education) #16.38095
mean(high_agriculture$Education) #6.615385
#calculating maxima and minima
swiss[swiss$Agriculture == max(swiss$Agriculture),]
swiss[swiss$Agriculture == min(swiss$Agriculture),]

Functions and class¶

Many R functions are written so that they behave differently depending on what class of variable they are given. For instance, the summary function gives additional information about a variable, and what it shows depends on the variable’s class.

# Class discrimination
x <- 1:10
summary(x)

data(swiss)
summary(swiss)

data(Titanic)
summary(Titanic)

So when a function does something unexpected, consider what mode or class the variables you gave it have.

Introduction to statistical functions in R¶

R also provides a large range of statistical functions. A commonly used one is the correlation function cor. Again, have a look at the documentation to learn what the input arguments for this function need to be.

#look at documentation
?cor

The documentation tells us that we need at least one argument x. The default correlation method is set to pearson. Let’s say we want to investigate if there is a correlation between fertility and catholic.

cor(swiss$Fertility, swiss$Catholic)

The function gives you a correlation 1x1 matrix. Your inputs do not necessarily have to be vectors, you can also input an entire matrix or data frame.

#correlation between the entire swiss data frame and fertility
cor(swiss, swiss$Fertility)

Next, we will change the correlation method (check out the documentation again to see which ones you can pick from).

#change method
cor(swiss$Fertility, swiss$Catholic, method = “spearman”)

You can also use R for significance testing. There is a huge amount of statistical tests available. We will only have a look at the t.test function at this point. Have a look at the iris data set.

#load iris data set
data(iris)
#iris data set
View(iris)

We now want to see if there is a significant difference in petal length between the two species setosa and versicolor. The t.test function calculates a “Welch Two samples t-test”.

#calculate t test
t.test(iris[iris$Species == "setosa",]$Petal.Length, iris[iris$Species == "versicolor",]$Petal.Length)

This will print out the summary of the t test in your consol. If you are planning on using the output for further calculation or simulations it makes sense to store the result in a variable.

#calculate t test and save in variable t_test
t_test <- t.test(iris[iris$Species == "setosa",]$Petal.Length, iris[iris$Species == "versicolor",]$Petal.Length)

The output is now stored as a list called t_test. You can easily access the different quantities using the dollar sign or double square brackets. For example, we can extract the t-statistic from our calculation

#get t-statistics
t_test$statistics
t_test[[statistics]]

To get an overview of all quantities provided by the function you can use the names function.

#overview over all quantities
names(t_test)

Exercise 0.8

Go back to your results in exercise 0.7. Are the results statistically significant?

Show how correlated are the infant mortality and the education level , than the correlation between the agricultural activity and the education level

cor(swiss$Infant.Mortality, swiss$Education) # -0.09932185 low correlation

cor(swiss$Agriculture, swiss$Education) # -0.639522 ,slight negative correlation -> higher education score lower agricultural activity

Using the same thresholds as Exercise 0.7 (10 for education, 50 for agriculture) , test whether there are statistically significant differences between :
The low and highly educated regions in infant mortality

#difference in mean between high and low education areas
low_education <- swiss[swiss$Education <= 10,]
high_education <- swiss[swiss$Education > 10,]
res_edu <- t.test(low_education$Infant.Mortality, high_education$Infant.Mortality)
res_edu$p.value # = 0.44, not significant

The regions with low and high agricultural activity and the education score

low_agriculture <- swiss[swiss$Agriculture <= 50,]
high_agriculture <- swiss[swiss$Agriculture > 50,]
res_agri <-t.test(low_agriculture$Education, high_agriculture$Education)
res_agri$p.value  # = 0.001394277, signficant difference

Program Flow¶

Without controls, a program will simply run from top to bottom, performing each command in turn. This would mean writing a lot of code if you wanted to perform the same set of actions on multiple different sets of data. Here we will learn how to control which parts of a program execute with if, and how to perform repetitive actions with the for loop.

The if function¶

An if function performs a logical test – is something TRUE? – and then runs commands if the test is passed.

# If function
x <- 4
if(x >= 0){
    y = sqrt(x)
}
y # = 2

Here, we only want to calculate the square root of x if x is positive.

We can extend the use of if to include a block of code to execute if something is FALSE.

# If / Else
x <- -2
if(x >= 0){
    y = sqrt(x)
}else{
    cat("The result would be a complex number!")
}
# The result would be a complex number!"

You can go further by making if dependent on multiple logic statements, or use recursive if statements.

# Only allow integer square roots
x <- 4.2
if((x >= 0) & (x%%1==0)){
    y = sqrt(x)
}else{
    cat("The result would not be an integer!")
}

# Alternative method
if(x >= 0){
    if(x%%1==0){
        y = sqrt(x)
    }else{
        cat("The result would not be an integer!")
    }
}else{
    cat("The result would be a complex number!")
}

Exercise 0.9

In the script window, copy the first if statement above and execute it. You should get the correct result, 2.
Now make x a negative value and execute the script again, what happens?
Add an else statement to your script as in the second example above and test it.
Using either multiple logic statements or nested if statements, write a script that tests whether x is an even square number.

# Script to determine is x is a square number
if(x%%2==0){
   y = sqrt(x)
   if(y%%1==0){
      cat(paste(x,"is even and the square of",y))
   }else{
      cat(paste(x,"is not a square number"))
   }
}else{
   cat(paste(x,"is not an even number"))
}

# Test it for yourself with different values of x!

The for loop¶

Whilst it’s very simple to run basic calculations on a vector or matrix of data, more sophisticated code is required for data.frames or when you want to perform complex functions on individual pieces of data.

The for loop is a basic programming concept that runs a series of commands through each loop, with one variable changing each time, which may or may not be used in the loop’s code. For instance we could loop through the numbers 1 to 10 if we wanted to perform an action 10 times, or if we wanted to use the numbers 1 to 10 each in the same calculation.

# A basic for loop
for(i in 1:10){
    cat("Loop!")
}
# Loop!Loop!Loop!Loop!Loop!Loop!Loop!Loop!Loop!Loop!

# A loop involving the loop variable
for(i in 1:10){
    cat(paste("Loop",i,"!"))
}
# Loop 1 !Loop 2 !Loop 3 !Loop 4 !Loop 5 !Loop 6 !Loop 7 !Loop 8 !Loop 9 !Loop 10 !

These are simple examples and don’t capture the results of the loop. If we want to store our results, we have to declare a variable ahead of time to put them into.

# A loop that gets results
data(EuStockMarkets)
plot(EuStockMarkets[,1])
movingAverage <- vector()
for(i in 1:length(EuStockMarkets[,1])){
    movingAverage[i] <- mean(EuStockMarkets[i:(i+29),1])
}
plot(movingAverage)

Note that an error was produced because when we reach the end of the time series, the data points we ask for don’t exist – we could adjust our loop to account for this by reducing the number of times we go through the loop so that we don’t reach past the end of the data.

Also, rather than refer to the pieces of data directly, we are using i to keep track of the index of the data we want to work with. This allows us to refer to data by its index, and therefore slice a moving section of data. In other circumstances, you can of course refer to items by their names.

Exercise 0.10

Write a for loop that prints out a countdown from 10 to 1.

# Countdown
for(i in 10:1){
   cat(i)
 }
 cat("Blast off!")

Using the EuStockMarkets data, make a plot of the FTSE data. Note that this data is not a data.frame but a time.series - you can find out more with ?ts.

# Plot FTSE data
data(EuStockMarkets)
plot(EuStockMarkets[,"FTSE"])
# Note that the $ syntax does not work with time.series objects

Using a for loop, calculate a moving average and make a corresponding vector of time points with the centres of each average.

# Calculate the moving average
movingAverage <- c()
for(i in 1:(length(EuStockMarkets[,"FTSE"])-29)){
   # Note that we avoid the error from earlier
   movingAverage[i] <- mean(EuStockMarkets[i:(i+29),"FTSE"])
}
times <- time(EuStockMarkets)[15:(length(EuStockMarkets[,"FTSE"])-15)]

Add the moving average to the plot using the lines function.

# Add to the plot
plot(EuStockMarkets[,"FTSE"])
lines(times,movingAverage,col=2)

Packages¶

We’ve so far used a lot of fundamental functions in R, the sort without which you couldn’t execute simple scripts at all. When performing data analysis however, there may well be better or more specific functions available for what you are trying to do. R is very flexible because it allows the loading of additional packages created by the user community to enhance and add functionality.

Loading a Package¶

Note: This section is unique to our Setup.

To load a package, we use the library function. Once loaded, all of the functions inside the package become available to R. If a function should have the identical name to an existing function, it will mask the current version and refer instead to the version in the package, and give you a warning. Note that a package can only be loaded if it is a native R package.

# Load the package and demonstrate
library(beeswarm)
random_numbers <- rnorm(100)
beeswarm(random_numbers)
beeswarm(random_numbers,method="hex")

Loading a Module¶

If the package has not been submitted to the standard R repositories, you cannot use the library function. You instead can call the module system on the server and load the software (if installed) manually using the module() function.

# Load a module
module("load prokka")

Note: the packages will be loaded permanently. If you want to unload a module you need to manually purge it

# Unload a module
module("purge prokka")

Apply() and tapply()¶

The apply() and tapply() functions are used to apply a certain function to a data frame, list, or vector and return the result as a list or a vector depending on the function we use.

The apply() function¶

The apply function is used to apply a certain function to the rows or columns of a matrix, data frame or array.

Syntax: apply(x, margin, function)

Parameters:
x: determines the input matrix, data frame, or array.
margin: 1 for rows, 2 for columns.
function: defines the function that is to be applied to each row (if margin = 1) or column (if margin = 2).

Let’s say we have a matrix mat and we want to calculate the sum of each column:

# Create the matrix
mat <- matrix(1:12, nrow = 4, ncol = 3)

# Apply the function
result <- apply(mat, 2, sum)

# Show results
print(result)

The tapply() function¶

The tapply function is used to apply a certain function to subsets of a vector or array based on a factor. It’s particularly useful for performing operations on data grouped by categories.

Syntax: tapply(x, index, function)

Parameters:
x: determines the input vector or an object.
index: a vector containing categories.
function: defines the function that is to be applied to each category.

Let’s say we have a vector of test scores and a factor indicating which class each score belongs to, and we want to calculate the mean score for each class:

# Create the data
scores <- c(85, 92, 78, 88, 90, 75, 82, 95, 89)
classes <- factor(c("A", "B", "A", "C", "B", "C", "A", "B", "C"))

# Apply the function
result <- tapply(scores, classes, mean)

# Show the results
print(result)

Data visualization with ggplot2¶

The package ggplot2 has a specific grammar for data visualization which uses three main entities:

the data: the data frame that contains the data that we want to plot
the aesthetics: the variables in the data that we want to be the dimensions of the plot (i.e. the x and y dimension, but also the color if we want to color-code according to a variable)
the geometric object (geom): specifies the type of plot we want to make (a scatter plot, a boxplot, an histogram, etc.)

The general notation of a plot is (DON’T EXECUTE):

ggplot(data,aes(x=aesthetic_1,y=aesthetic_2)) +
  geom_*()

Let’s see a basic example. We’ll use the iris dataset as the data and will plot a scatterplot (that is the geom) with Sepal.Length and Petal.Length as the x and y dimensions (that is the aesthetics):

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length)) +
  geom_point()

You can have a look to the Data Visualization cheatsheet (https://rstudio.com/wp-content/uploads/2015/03/ggplot2-cheatsheet.pdf) which is a good one-page summary of the main functions.

Aesthetics¶

We can add more aesthetics than just the x and y dimensions. For example we can plot the information of a 3rd variable (Species for example) as the color of the dots, or as the shape. ggplot2 will handle it easily and will produce a legend automatically:

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length,col=Species)) +
  geom_point()

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length,shape=Species)) +
  geom_point()

Geometric objects¶

We can tune the type of plot by choosing the appropiate geometric object. Let’s make an histogram and a boxplot of the sepal length by species. You will have to change the aesthetics accordingly: note that the histogram won’t need a y aesthetic and the collor is defined with fill (instead of col).

ggplot(data=iris,aes(x=Sepal.Length,fill=Species)) +
  geom_histogram()

ggplot(data=iris,aes(x=Species,y=Sepal.Length,fill=Species)) +
  geom_boxplot()

Other layers¶

We can further tune the plot by adding more layers that will add new features to the plot.

First, we’ll see how we can add a linear fit to the scatter plot:

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length)) +
  geom_point() +
  geom_smooth(method="lm")

We can re-write the axis labels and add a title and subtitle:

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length,col=Species)) +
  geom_point() +
  geom_smooth(method="lm") +
  xlab("Sepal length (cm)") +
  ylab("Petal length (cm)") +
  labs(title="Fisher's or Anderson's iris dataset",subtitle = "Content: 50 flowers from each of 3 species of iris")

We can also tune the general style of the plot by setting a different theme:

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length,col=Species)) +
  geom_point() +
  geom_smooth(method="lm") +
  xlab("Sepal length (cm)") +
  ylab("Petal length (cm)") +
  labs(title="Fisher's or Anderson's iris dataset",subtitle = "Content: 50 flowers from each of 3 species of iris") +
  theme_minimal()

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length,col=Species)) +
  geom_point() +
  geom_smooth(method="lm") +
  xlab("Sepal length (cm)") +
  ylab("Petal length (cm)") +
  labs(title="Fisher's or Anderson's iris dataset",subtitle = "Content: 50 flowers from each of 3 species of iris") +
  theme_classic()

Finally, we can easily more than one plot with a single ggplot command if we can split the dataset according to a variable, for example the Species:

ggplot(data=iris,aes(x=Sepal.Length,y=Petal.Length,col=Species)) +
  geom_point() +
  geom_smooth(method="lm") +
  xlab("Sepal length (cm)") +
  ylab("Petal length (cm)") +
  labs(title="Fisher's or Anderson's iris dataset",subtitle = "Content: 50 flowers from each of 3 species of iris") +
  theme_minimal() +
  facet_wrap(~Species)

Exercise 0.11

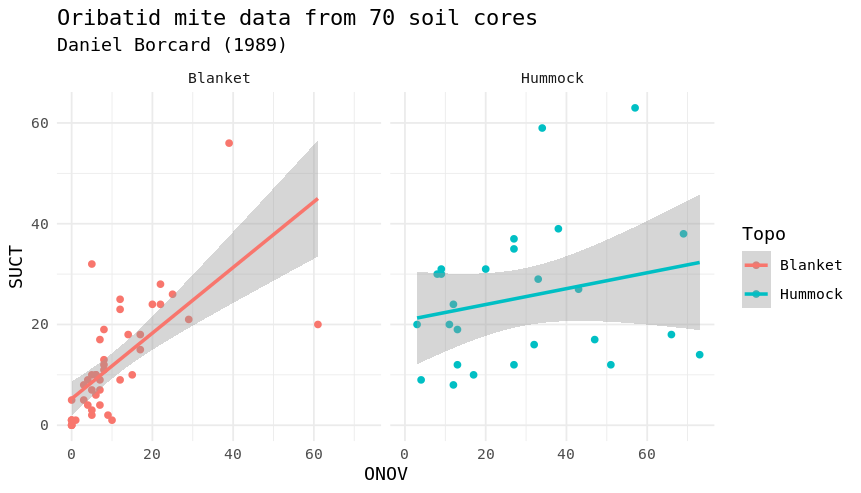
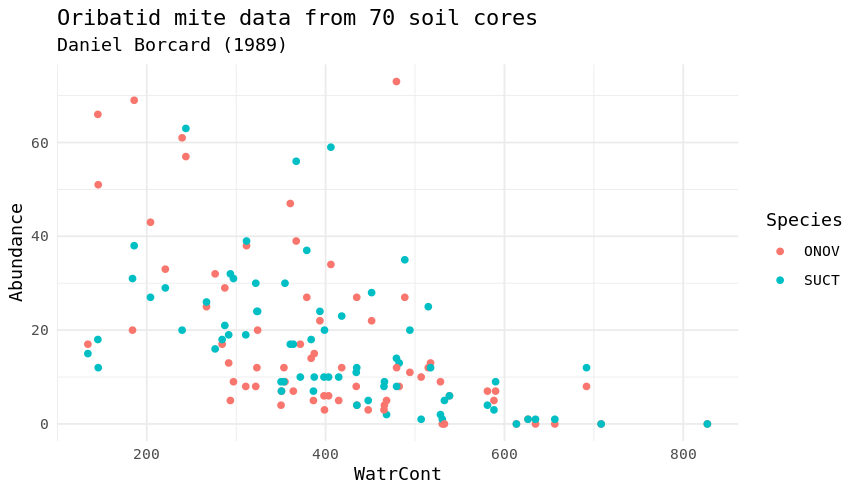
Load the mite and mite.env datasets from the vegan package (you will have to load the “vegan” package first) and try to reproduce the two plots underneath (additionally we used the package “tidyverse” and “ggplot2”). The mite dataset contains information on Oribatid mite data from 70 soil cores collected by Daniel Borcard in 1989. The mite data frame contains the species abundances and the mite.env contains environmental information. Note that you will have to transform the data differently for each plot.

library("vegan")
library("tidyverse")
library("ggplot2")

data(mite)
data(mite.env)

mite<-mite %>%
  rownames_to_column(var="site")

mite.env<-mite.env %>%
  rownames_to_column(var="site")

mite.all<-mite %>%
  left_join(mite.env,by="site")

ggplot(data=mite.all,aes(x=ONOV,y=SUCT,col=Topo)) +
  geom_point() +
  geom_smooth(method="lm") +
  labs(title="Oribatid mite data from 70 soil cores",subtitle = "Daniel Borcard (1989)") +
  theme_minimal() +
  facet_wrap(~Topo)

mite.all.long<-mite %>%
  pivot_longer(-site,names_to = "Species",values_to = "Abundance") %>%
  left_join(mite.env,by="site") %>%
  filter(Species %in% c("ONOV","SUCT"))

ggplot(data=mite.all.long,aes(x=WatrCont,y=Abundance,col=Species)) +
  geom_point() +
  labs(title="Oribatid mite data from 70 soil cores",subtitle = "Daniel Borcard (1989)") +
  theme_minimal()

Next: Refresher - Python/Jupyter